Recursive definition:
A definition in which something is defined in terms of a smaller
version of itself.
From the previous example (factorial), it is clear that:
1. Every recursive definition must have one (or more) base cases.
2. The general case must eventually be reduced to a base case.
3. The base case stops the recursion.
The concept of recursion in computer science works similarly. Here, we talk about recursive
algorithms and recursive functions. An algorithm that finds the solution to a given problem
by reducing the problem to smaller versions of itself is called a recursive algorithm. The
recursive algorithm must have one or more base cases, and the general solution must
eventually be reduced to a base case.
A function that calls itself is called a recursive function. That is, the body of the
recursive function contains a statement that causes the same function to execute again
before completing the current call. Recursive algorithms are implemented using recursive
functions.
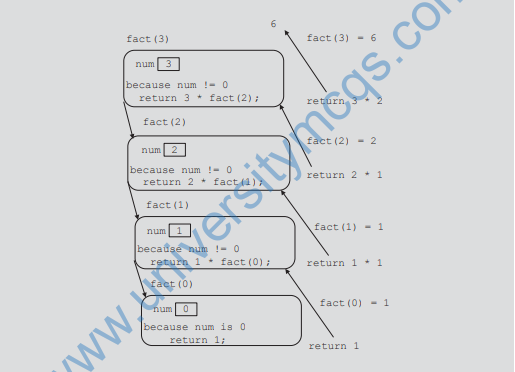
Next, let us write the recursive function that implements the factorial function.
int fact(int num)
{
if (num == 0)
return 1;
else
return num * fact(num – 1);
}
cout << fact(3) << endl;
The output of the previous cout statement is: 6
To design a recursive function, you must do the following:
1. Understand the problem requirements.
2. Determine the limiting conditions. For example, for a list, the limiting condition
is the number of elements in the list.
3. Identify the base cases and provide a direct solution to each base case.
4. Identify the general cases and provide a solution to each general case in terms of
smaller versions of itself.
Tower of Hanoi
In the nineteenth century, a game called the Tower of Hanoi became popular in Europe.
This game represents work that is under way in the temple of Brahma. At the creation of
the universe, priests in the temple of Brahma were supposedly given three diamond
needles, with one needle containing 64 golden disks. Each golden disk is slightly smaller
than the disk below it. The priests’ task is to move all 64 disks from the first needle to the
third needle. The rules for moving the disks are as follows:
1. Only one disk can be moved at a time.
2. The removed disk must be placed on one of the needles.
3. A larger disk cannot be placed on top of a smaller disk.
The priests were told that once they had moved all the disks from the first needle to the
third needle, the universe would come to an end.As before, we think in terms of recursion. Let us first consider the case when the first
needle contains only one disk. In this case, the disk can be moved directly from
needle 1 to needle 3. So let us consider the case when the first needle contains only
two disks. In this case, first we move the first disk from needle 1 to needle 2, and
then we move the second disk from needle 1 to needle 3. Finally, we move the first
disk from needle 2 to needle 3. Next, we consider the case when the first needle
contains three disks, and then generalize this to the case of 64 disks (in fact, to an
arbitrary number of disks).
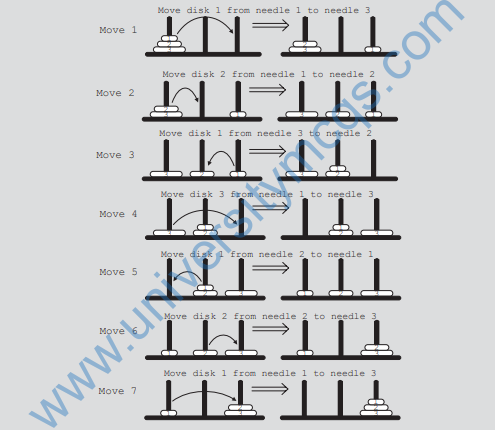
Suppose that needle 1 contains three disks. To move disk number 3 to needle 3, the top
two disks must first be moved to needle 2. Disk number 3 can then be moved from
needle 1 to needle 3. To move the top two disks from needle 2 to needle 3, we use the
same strategy as before. This time we use needle 1 as the intermediate needle.
Converting a Number from Decimal to Binary using recursion:
#include <iostream>
using namespace std;
void decToBin(int num, int base);
int main()
{
int decimalNum;
int base;
base = 2;
cout << “Enter number in decimal: “;
cin >> decimalNum;
cout << endl;
cout << “Decimal ” << decimalNum << ” = “;
decToBin(decimalNum, base);
cout << ” binary” << endl;
return 0;
}
void decToBin(int num, int base)
{
if (num > 0)
{
decToBin(num / base, base);
cout << num % base;
}
}
Sample Run: In this sample run, the user input is shaded.
Enter a number in decimal: 57
Decimal 57 = 111001 binary

