Stack:
A data structure in which the elements are added and removed from one end
only, a Last In First Out (LIFO) data structure.
Now that you know what a stack is, let us see what kinds of operations can be performed
on a stack. Because new items can be added to the stack, we can perform the add
operation, called push, to add an element onto the stack. Similarly, because the top item
can be retrieved and/or removed from the stack, we can perform the operation top to
retrieve the top element of the stack, and the operation pop to remove the top element
from the stack.
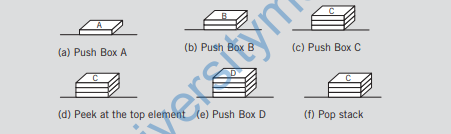
The push, top, and pop operations work as follows: Suppose there are boxes lying on
the floor that need to be stacked on a table. Initially, all of the boxes are on the floor and
the stack is empty.
First we push box A onto the stack. After the push operation,
the stack is as shown in figure below
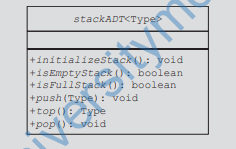
• initializeStack—Initializes the stack to an empty state.
• isEmptyStack—Determines whether the stack is empty. If the stack
is empty, it returns the value true; otherwise, it returns the value
false.
• isFullStack—Determines whether the stack is full. If the stack is full, it
returns the value true; otherwise, it returns the value false.
• push—Adds a new element to the top of the stack. The input to this
operation consists of the stack and the new element. Prior to this operation, the stack must exist and must not be full.
• top—Returns the top element of the stack. Prior to this operation, the
stack must exist and must not be empty.
• pop—Removes the top element of the stack. Prior to this operation, the
stack must exist and must not be empty
Empty Stack
We have seen that the value of stackTop indicates whether the stack is empty. If
stackTop is 0, the stack is empty; otherwise, the stack is not empty. The definition of
the function isEmptyStack is as follows:
template <class Type>
bool stackType<Type>::isEmptyStack() const
{
return(stackTop == 0);
}//end isEmptyStack
Full Stack
Next, we consider the operation isFullStack. It follows that the stack is full if stackTop
is equal to maxStackSize. The definition of the function isFullStack is as follows:
template <class Type>
bool stackType<Type>::isFullStack() const
{
return(stackTop == maxStackSize);
} //end isFullStack
Push:
Adding, or pushing, an element onto the stack is a two-step process. Recall that the value
of stackTop indicates the number of elements in the stack, and stackTop – 1 gives the
position of the top element of the stack. Therefore, the push operation is as follows:
1. Store the newItem in the array component indicated by stackTop.
2. Increment stackTop.
The definition of the function push is as follows:
template <class Type>
void stackType<Type>::push(const Type& newItem)
{
if (!isFullStack())
{
list[stackTop] = newItem; //add newItem at the top
stackTop++; //increment stackTop
}
else
cout << “Cannot add to a full stack.” << endl;
}//end push
If we try to add a new item to a full stack, the resulting condition is called an overflow.
Error checking for an overflow can be handled in different ways. One way is as shown
previously. Or, we can check for an overflow before calling the function push, as shown
next (assuming stack is an object of type stackType).
if (!stack.isFullStack())
stack.push(newItem);
Return the Top Element:
The operation top returns the top element of the stack. Its definition is as follows:
template <class Type>
Type stackType<Type>::top() const
{
assert(stackTop != 0); //if stack is empty, terminate the
//program
return list[stackTop – 1]; //return the element of the stack
//indicated by stackTop – 1
}//end top
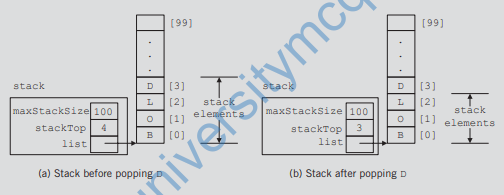
Pop:
To remove, or pop, an element from the stack, we simply decrement stackTop by 1.
The definition of the function pop is as follows:
template <class Type>
void stackType<Type>::pop()
{
if (!isEmptyStack())
stackTop–; //decrement stackTop
else
cout << “Cannot remove from an empty stack.” << endl;
}//end pop
If we try to remove an item from an empty stack, the resulting condition is called an underflow. Error checking for an underflow can be handled in different ways. One way
is as shown previously. Or, we can check for an underflow before calling the function
pop, as shown next (assuming stack is an object of type stackType).
if (!stack.isEmptyStack())
stack.pop();
STACK FULL CODE:
#include<iostream>
using namespace std;
const int size = 3;
int stackB[size];
int top = -1;
bool isEmpty(){
if(top == -1){
cout<<“Stack is empty”<<endl;
return true;
}
else
return false;
}
bool isFull(){
if(top == size – 1){
cout<<“Stack is full”<<endl;
return true;
}
else
return false;
}
void push(int a){
if(isFull()){
cout<<“Sorry! the stack is already full.”<<endl;
}
else{
top++;
stackB[top] = a;
cout<<a<<” has been pushed to the stack”<<endl;
}
}
void pop(){
if(isEmpty()){
cout<<“Error! there is no data on the stack”<<endl;
}
else{
int temp = stackB[top];
top–;
cout<<temp<<” has been removed from the stack”<<endl;
}
}
int main(){
isEmpty();
push(90);
push(80);
push(70);
isFull();
pop();
pop();
pop();
isEmpty();
return 0;
}

