Examples of TM
Example 1:
Construct a TM for the language L = {0n1n2n} where n≥1
Solution:
L = {0n1n2n | n≥1} represents language where we use only 3 character, i.e., 0, 1 and 2. In this, some number of 0’s followed by an equal number of 1’s and then followed by an equal number of 2’s. Any type of string which falls in this category will be accepted by this language.
The simulation for 001122 can be shown as below:

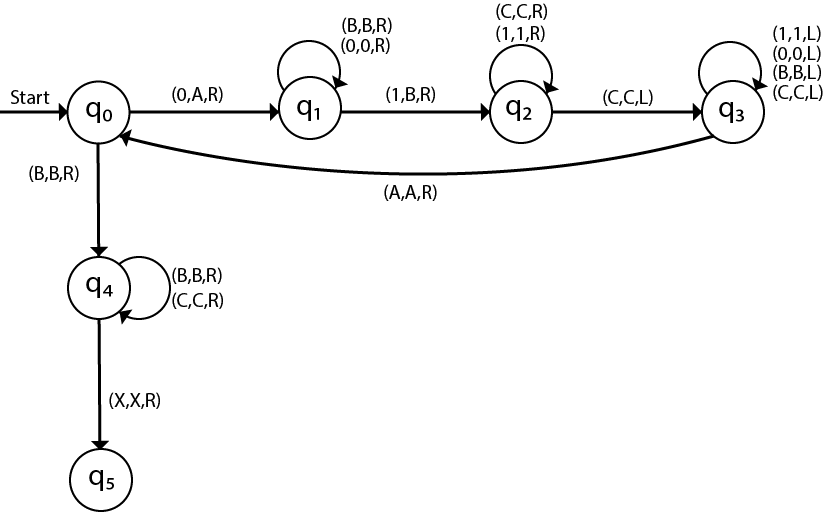
Now, we will see how this Turing machine will work for 001122. Initially, state is q0 and head points to 0 as:

The move will be δ(q0, 0) = δ(q1, A, R) which means it will go to state q1, replaced 0 by A and head will move to the right as:

The move will be δ(q1, 0) = δ(q1, 0, R) which means it will not change any symbol, remain in the same state and move to the right as:

The move will be δ(q1, 1) = δ(q2, B, R) which means it will go to state q2, replaced 1 by B and head will move to right as:

The move will be δ(q2, 1) = δ(q2, 1, R) which means it will not change any symbol, remain in the same state and move to right as:

The move will be δ(q2, 2) = δ(q3, C, R) which means it will go to state q3, replaced 2 by C and head will move to right as:

Now move δ(q3, 2) = δ(q3, 2, L) and δ(q3, C) = δ(q3, C, L) and δ(q3, 1) = δ(q3, 1, L) and δ(q3, B) = δ(q3, B, L) and δ(q3, 0) = δ(q3, 0, L), and then move δ(q3, A) = δ(q0, A, R), it means will go to state q0, replaced A by A and head will move to right as:

The move will be δ(q0, 0) = δ(q1, A, R) which means it will go to state q1, replaced 0 by A, and head will move to right as:

The move will be δ(q1, B) = δ(q1, B, R) which means it will not change any symbol, remain in the same state and move to right as:

The move will be δ(q1, 1) = δ(q2, B, R) which means it will go to state q2, replaced 1 by B and head will move to right as:

The move will be δ(q2, C) = δ(q2, C, R) which means it will not change any symbol, remain in the same state and move to right as:

The move will be δ(q2, 2) = δ(q3, C, L) which means it will go to state q3, replaced 2 by C and head will move to left until we reached A as:

immediately before B is A that means all the 0’s are market by A. So we will move right to ensure that no 1 or 2 is present. The move will be δ(q2, B) = (q4, B, R) which means it will go to state q4, will not change any symbol, and move to right as:

The move will be (q4, B) = δ(q4, B, R) and (q4, C) = δ(q4, C, R) which means it will not change any symbol, remain in the same state and move to right as:

The move δ(q4, X) = (q5, X, R) which means it will go to state q5 which is the HALT state and HALT state is always an accept state for any TM.

The same TM can be represented by Transition Diagram:
Example 2:
Construct a TM machine for checking the palindrome of the string of even length.
Solution:
Firstly we read the first symbol from the left and then we compare it with the first symbol from right to check whether it is the same.
Again we compare the second symbol from left with the second symbol from right. We repeat this process for all the symbols. If we found any symbol not matching, we cannot lead the machine to HALT state.
Suppose the string is ababbabaΔ. The simulation for ababbabaΔ can be shown as follows:

Now, we will see how this Turing machine will work for ababbabaΔ. Initially, state is q0 and head points to a as:

We will mark it by * and move to right end in search of a as:

We will move right up to Δ as:

We will move left and check if it is a:

It is ‘a’ so replace it by Δ and move left as:

Now move to left up to * as:

Move right and read it

Now convert b by * and move right as:

Move right up to Δ in search of b as:

Move left, if the symbol is b then convert it into Δ as:

Now move left until * as:

Replace a by * and move right up to Δ as:

We will move left and check if it is a, then replace it by Δ as:

It is ‘a’ so replace it by Δ as:
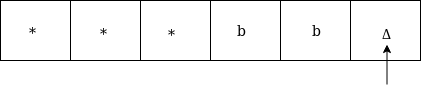
Now move left until *
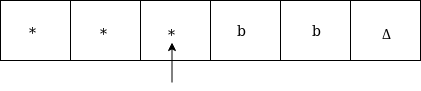
Now move right as:
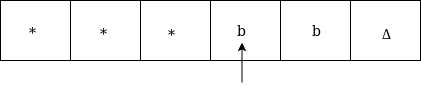
Replace b by * and move right up to Δ as:
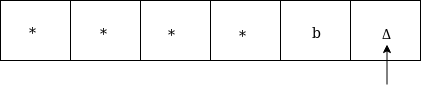
Move left, if the left symbol is b, replace it by Δ as:
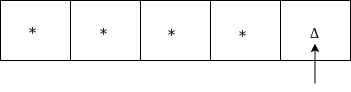
Move left till *
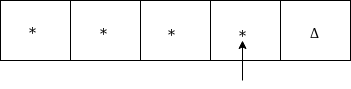
Move right and check whether it is Δ
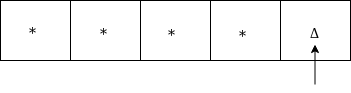
Go to HALT state
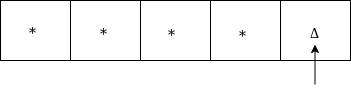
The same TM can be represented by Transition Diagram:
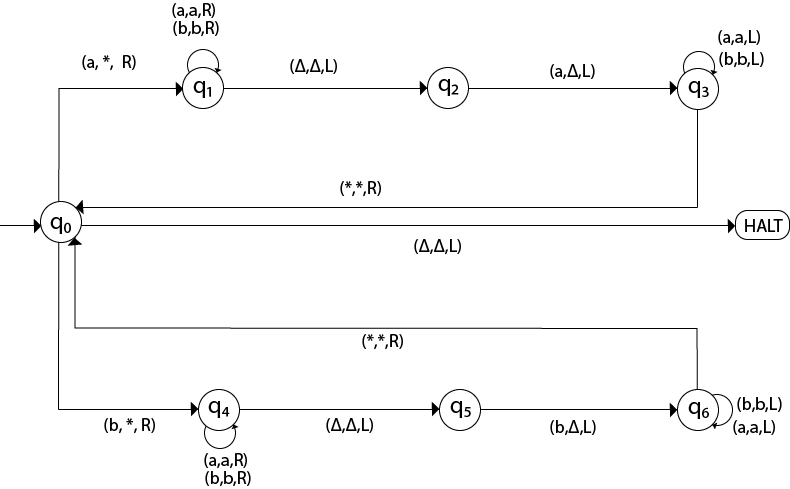
Example 3:
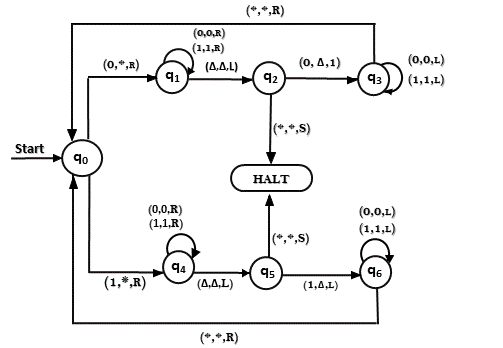
Construct a TM machine for checking the palindrome of the string of odd length.
Solution:
Firstly we read the first symbol from left and then we compare it with the first symbol from right to check whether it is the same.
Again we compare the second symbol from left with the second symbol from right. We repeat this process for all the symbols. If we found any symbol not matching, we lead the machine to HALT state.
Suppose the string is 00100Δ. The simulation for 00100Δ can be shown as follows:
Now, we will see how this Turing machine will work for 00100Δ. Initially, state is q0 and head points to 0 as:
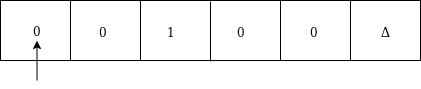
Now replace 0 by * and move right as:
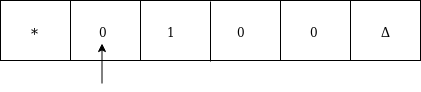
Move right up to Δ as:
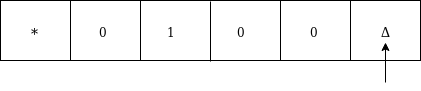
Move left and replace 0 by Δ and move left:
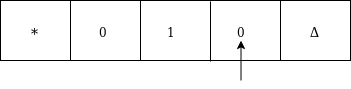
Now move left up to * as:

Move right, convert 0 by * and then move right as:
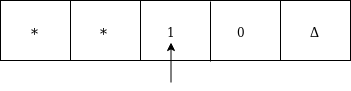
Moved right up to Δ

Move left and replace 0 by Δ as:

Move left till * as:

Move right and convert 1 to * as:
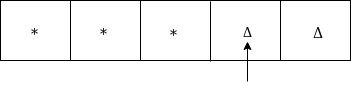
Move left
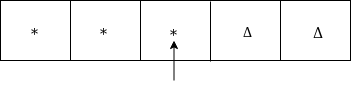
Since it is *, goto HALT state.
The same TM can be represented by Transition Diagram:
Example 4:
Construct TM for the addition function for the unary number system.
Solution:
The unary number is made up of only one character, i.e. The number 5 can be written in unary number system as 11111. In this TM, we are going to perform the addition of two unary numbers.
For example
2 + 3
i.e. 11 + 111 = 11111
If you observe this process of addition, you will find the resemblance with string concatenation function.
In this case, we simply replace + by 1 and move ahead right for searching end of the string we will convert last 1 to Δ.
Input: 3+2
The simulation for 111+11Δ can be shown as below:

Move right up to + sign as:

Convert + to 1 and move right as:

Now, move right

Again move right

Now Δ has encountered, so just move left as:

Convert 1 to Δ

Thus the tape now consists of the addition of two unary numbers.
The TM will look like as follows:
Here, we are implementing the function of f(a + b) = c. We assume a and b both are non zero elements.
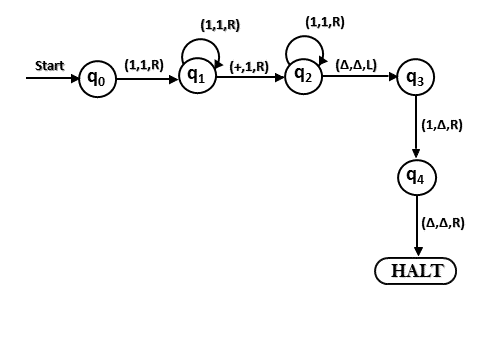
Example 5:
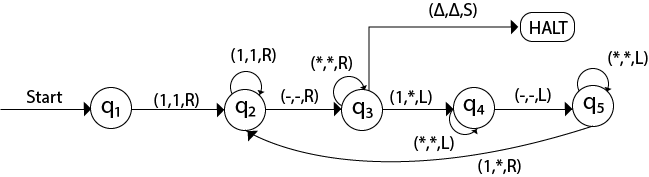
Construct a TM for subtraction of two unary numbers f(a-b) = c where a is always greater than b.
Solution: Here we have certain assumptions as the first number is greater than the second one. Let us assume that a = 3, b = 2, so the input tape will be:

We will move right to – symbol as perform reduction of a number of 1’s from the first number. Let us look at the simulation for understanding the logic:

Move right up to – as:

Move right and convert 1 to * as:

Now move left

Again move left

Convert 1 to * and move right-hand

Now move right till 1

Convert 1 to * and move left

Convert 1 to * and move


Move right till Δ as:

Now we are in the HALT state.
Thus we get 1 on the input tape as the answer for f(3-2).
The Turing machine will look like this:
- Theory of Automata
- Finite Automata
- Transition Diagram
- Transition Table
- DFA (Deterministic finite automata)
- Examples of DFA
- NFA (Non-Deterministic finite automata)
- Examples of NFA
- Eliminating ε Transitions
- Conversion from NFA to DFA
- Conversion from NFA with ε to DFA
- Minimization of DFA
- Regular Expression
- Examples of Regular Expression
- Moore Machine
- Mealy Machine
- Context Free Grammar
- Simplification of CFG
- Chomsky’s Normal Form (CNF)
- Greibach Normal Form (GNF)
- Pushdown Automata(PDA)
- Non-deterministic Pushdown Automata
- Turing Machine
- Examples of TM



