Non-deterministic Pushdown Automata
The non-deterministic pushdown automata is very much similar to NFA. We will discuss some CFGs which accepts NPDA.
The CFG which accepts deterministic PDA accepts non-deterministic PDAs as well. Similarly, there are some CFGs which can be accepted only by NPDA and not by DPDA. Thus NPDA is more powerful than DPDA.
Example:
Design PDA for Palindrome strips.
Solution:
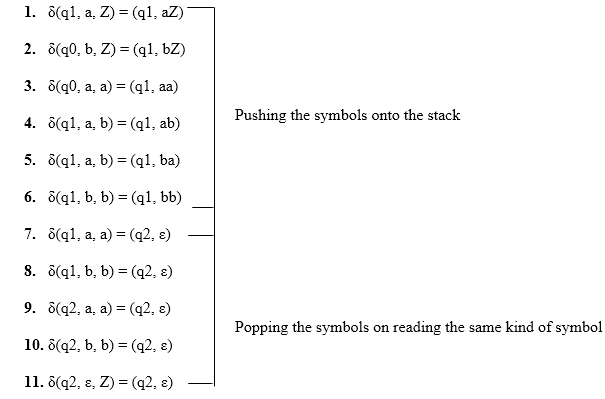
Suppose the language consists of string L = {aba, aa, bb, bab, bbabb, aabaa, ……]. The string can be odd palindrome or even palindrome. The logic for constructing PDA is that we will push a symbol onto the stack till half of the string then we will read each symbol and then perform the pop operation. We will compare to see whether the symbol which is popped is similar to the symbol which is read. Whether we reach to end of the input, we expect the stack to be empty.
This PDA is a non-deterministic PDA because finding the mid for the given string and reading the string from left and matching it with from right (reverse) direction leads to non-deterministic moves. Here is the ID.
Simulation of abaaba
- δ(q1, abaaba, Z) Apply rule 1
- ⊢ δ(q1, baaba, aZ) Apply rule 5
- ⊢ δ(q1, aaba, baZ) Apply rule 4
- ⊢ δ(q1, aba, abaZ) Apply rule 7
- ⊢ δ(q2, ba, baZ) Apply rule 8
- ⊢ δ(q2, a, aZ) Apply rule 7
- ⊢ δ(q2, ε, Z) Apply rule 11
- ⊢ δ(q2, ε) Accept
- Theory of Automata
- Finite Automata
- Transition Diagram
- Transition Table
- DFA (Deterministic finite automata)
- Examples of DFA
- NFA (Non-Deterministic finite automata)
- Examples of NFA
- Eliminating ε Transitions
- Conversion from NFA to DFA
- Conversion from NFA with ε to DFA
- Minimization of DFA
- Regular Expression
- Examples of Regular Expression
- Moore Machine
- Mealy Machine
- Context Free Grammar
- Simplification of CFG
- Chomsky’s Normal Form (CNF)
- Greibach Normal Form (GNF)
- Pushdown Automata(PDA)
- Non-deterministic Pushdown Automata
- Turing Machine
- Examples of TM

