- Finite automata are used to recognize patterns.
- It takes the string of symbol as input and changes its state accordingly. When the desired symbol is found, then the transition occurs.
- At the time of transition, the automata can either move to the next state or stay in the same state.
- Finite automata have two states, Accept state or Reject state. When the input string is processed successfully, and the automata reached its final state, then it will accept.
Formal Definition of FA
A finite automaton is a collection of 5-tuple (Q, ∑, δ, q0, F), where:
- Q: finite set of states
- ∑: finite set of the input symbol
- q0: initial state
- F: final state
- δ: Transition function
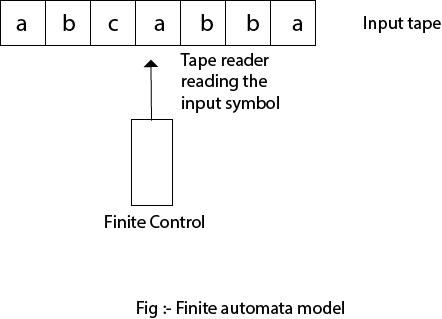
Finite Automata Model:
Finite automata can be represented by input tape and finite control.
Input tape: It is a linear tape having some number of cells. Each input symbol is placed in each cell.
Finite control: The finite control decides the next state on receiving particular input from input tape. The tape reader reads the cells one by one from left to right, and at a time only one input symbol is read.
Types of Automata:
There are two types of finite automata:
- DFA(deterministic finite automata)
- NFA(non-deterministic finite automata)
1. DFA
DFA refers to deterministic finite automata. Deterministic refers to the uniqueness of the computation. In the DFA, the machine goes to one state only for a particular input character. DFA does not accept the null move.
2. NFA
NFA stands for non-deterministic finite automata. It is used to transmit any number of states for a particular input. It can accept the null move.
Some important points about DFA and NFA:
- Every DFA is NFA, but NFA is not DFA.
- There can be multiple final states in both NFA and DFA.
- DFA is used in Lexical Analysis in Compiler.
- NFA is more of a theoretical concept.
- Theory of Automata
- Finite Automata
- Transition Diagram
- Transition Table
- DFA (Deterministic finite automata)
- Examples of DFA
- NFA (Non-Deterministic finite automata)
- Examples of NFA
- Eliminating ε Transitions
- Conversion from NFA to DFA
- Conversion from NFA with ε to DFA
- Minimization of DFA
- Regular Expression
- Examples of Regular Expression
- Moore Machine
- Mealy Machine
- Context Free Grammar
- Simplification of CFG
- Chomsky’s Normal Form (CNF)
- Greibach Normal Form (GNF)
- Pushdown Automata(PDA)
- Non-deterministic Pushdown Automata
- Turing Machine
- Examples of TM


