Minimization of DFA means reducing the number of states from given FA. Thus, we get the FSM(finite state machine) with redundant states after minimizing the FSM.
We have to follow the various steps to minimize the DFA. These are as follows:
Step 1: Remove all the states that are unreachable from the initial state via any set of the transition of DFA.
Step 2: Draw the transition table for all pair of states.
Step 3: Now split the transition table into two tables T1 and T2. T1 contains all final states, and T2 contains non-final states.
Step 4: Find similar rows from T1 such that:
- 1. δ (q, a) = p
- 2. δ (r, a) = p
That means, find the two states which have the same value of a and b and remove one of them.
Step 5: Repeat step 3 until we find no similar rows available in the transition table T1.
Step 6: Repeat step 3 and step 4 for table T2 also.
Step 7: Now combine the reduced T1 and T2 tables. The combined transition table is the transition table of minimized DFA.
Example:
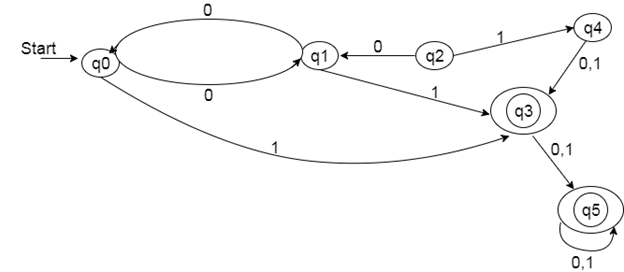
Solution:
Step 1: In the given DFA, q2 and q4 are the unreachable states so remove them.
Step 5: In set 2, row 1 and row 2 are similar since q3 and q5 transit to the same state on 0 and 1. So skip q5 and then replace q5 by q3 in the rest.
| State | 0 | 1 |
|---|---|---|
| q3 | q3 | q3 |
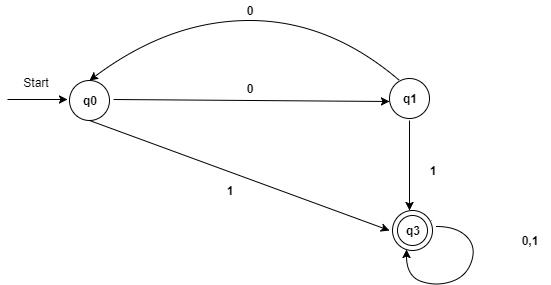
Step 6: Now combine set 1 and set 2 as:
| State | 0 | 1 |
|---|---|---|
| →q0 | q1 | q3 |
| q1 | q0 | q3 |
| *q3 | q3 | q3 |
Now it is the transition table of minimized DFA.
- Theory of Automata
- Finite Automata
- Transition Diagram
- Transition Table
- DFA (Deterministic finite automata)
- Examples of DFA
- NFA (Non-Deterministic finite automata)
- Examples of NFA
- Eliminating ε Transitions
- Conversion from NFA to DFA
- Conversion from NFA with ε to DFA
- Minimization of DFA
- Regular Expression
- Examples of Regular Expression
- Moore Machine
- Mealy Machine
- Context Free Grammar
- Simplification of CFG
- Chomsky’s Normal Form (CNF)
- Greibach Normal Form (GNF)
- Pushdown Automata(PDA)
- Non-deterministic Pushdown Automata
- Turing Machine
- Examples of TM


