Eliminating ε Transitions
NFA with ε can be converted to NFA without ε, and this NFA without ε can be converted to DFA. To do this, we will use a method, which can remove all the ε transition from given NFA. The method will be:
- Find out all the ε transitions from each state from Q. That will be called as ε-closure{q1} where qi ∈ Q.
- Then δ’ transitions can be obtained. The δ’ transitions mean a ε-closure on δ moves.
- Repeat Step-2 for each input symbol and each state of given NFA.
- Using the resultant states, the transition table for equivalent NFA without ε can be built.
Example:
Convert the following NFA with ε to NFA without ε.
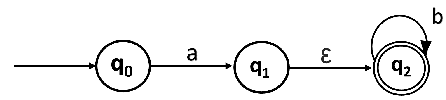
Solutions: We will first obtain ε-closures of q0, q1 and q2 as follows:
- ε-closure(q0) = {q0}
- ε-closure(q1) = {q1, q2}
- ε-closure(q2) = {q2}
Now the δ’ transition on each input symbol is obtained as:δ'(q0, a) = ε-closure(δ(δ^(q0, ε),a))
- = ε-closure(δ(ε-closure(q0),a))
- = ε-closure(δ(q0, a))
- = ε-closure(q1)
- = {q1, q2}
- δ'(q0, b) = ε-closure(δ(δ^(q0, ε),b))
- = ε-closure(δ(ε-closure(q0),b))
- = ε-closure(δ(q0, b))
- = Ф
Now the δ’ transition on q1 is obtained as:
- δ'(q1, a) = ε-closure(δ(δ^(q1, ε),a))
- = ε-closure(δ(ε-closure(q1),a))
- = ε-closure(δ(q1, q2), a)
- = ε-closure(δ(q1, a) ∪ δ(q2, a))
- = ε-closure(Ф ∪ Ф)
- = Ф
- δ'(q1, b) = ε-closure(δ(δ^(q1, ε),b))
- = ε-closure(δ(ε-closure(q1),b))
- = ε-closure(δ(q1, q2), b)
- = ε-closure(δ(q1, b) ∪ δ(q2, b))
- = ε-closure(Ф ∪ q2)
- = {q2}
The δ’ transition on q2 is obtained as:
- δ'(q2, a) = ε-closure(δ(δ^(q2, ε),a))
- = ε-closure(δ(ε-closure(q2),a))
- = ε-closure(δ(q2, a))
- = ε-closure(Ф)
- = Ф
- δ'(q2, b) = ε-closure(δ(δ^(q2, ε),b))
- = ε-closure(δ(ε-closure(q2),b))
- = ε-closure(δ(q2, b))
- = ε-closure(q2)
- = {q2}
Now we will summarize all the computed δ’ transitions:
- δ'(q0, a) = {q0, q1}
- δ'(q0, b) = Ф
- δ'(q1, a) = Ф
- δ'(q1, b) = {q2}
- δ'(q2, a) = Ф
- δ'(q2, b) = {q2}
The transition table can be:
| States | a | b |
|---|---|---|
| →q0 | {q1, q2} | Ф |
| *q1 | Ф | {q2} |
| *q2 | Ф | {q2} |
State q1 and q2 become the final state as ε-closure of q1 and q2 contain the final state q2. The NFA can be shown by the following transition diagram:
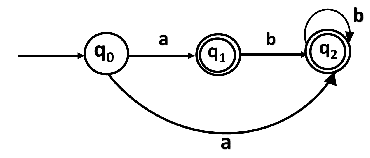
- Theory of Automata
- Finite Automata
- Transition Diagram
- Transition Table
- DFA (Deterministic finite automata)
- Examples of DFA
- NFA (Non-Deterministic finite automata)
- Examples of NFA
- Eliminating ε Transitions
- Conversion from NFA to DFA
- Conversion from NFA with ε to DFA
- Minimization of DFA
- Regular Expression
- Examples of Regular Expression
- Moore Machine
- Mealy Machine
- Context Free Grammar
- Simplification of CFG
- Chomsky’s Normal Form (CNF)
- Greibach Normal Form (GNF)
- Pushdown Automata(PDA)
- Non-deterministic Pushdown Automata
- Turing Machine
- Examples of TM
Post Views: 1,189


